드디어 마지막 장 까지 도달하였다. 책 이론들을 정리만 하는데 그치지 않고, 문제들을 풀면서 계속해서 복습해 나갈 예정이다.

다이나믹 프로그래밍

최적 부분 구조를 갖고 있는 문제를 DP로 풀이가 가능하다. 최적 부분 구조를 푸는 또 다른 알고리즘으로는 그리디 알고리즘이 있다. 그리디는 항상 그 순간에 최적이라고 생각되는 것을 선택하면서 문제를 푸는 방식이고, DP는 중복된 하위 문제들의 결과를 저장해뒀다가 풀이해 나간다는 차이가 있다. 여기서 중요한 점은 중복된 문제들이란 점이며, 중복되지 않는 문제들은 DP로 풀지 않는다. 대표적으로 병합 정렬과 퀵 정렬 등이 있으며, 이들은 모두 분할 정복 알고리즘으로 분류한다.대부분의 재귀 알고리즘은 최적 부분 구조 문제를 풀 수 있다. 이 중에서도 병합 정렬, 퀵 정렬과 같은 분할 정복 알고리즘은 중복된 하위 문제들 을 푸는 것이 아니기 떄문에 DP로 분류하지 않는다. 배낭 문제 중 분할 가능 배낭 문제는 탐욕 선택 속성이 있기 떄문에 그리디 알고리즘으로 풀이할 수 있다.

13장의 다익스트라 알고리즘은 DP와 그리디에 둘 다 해당하는 경우인데, BFS 시 항상 최단 경로를 찾고 탐욕 선택 속성을 갖는 그리디 알고리즘이면서, 이미 계산한 경로를 저장해두었다가 활용하며 중복된 하위 문제들을 푸는 DP 이기도 하다.
즉, 다익스트라 알고리즘은 최적 부분 구조, 중복된 하위 문제들, 탐욕 선택 속성을 모두 갖는 문제이다.

최적 부분 구조

최적 부분 구조에 대해 좀 더 살펴보자.
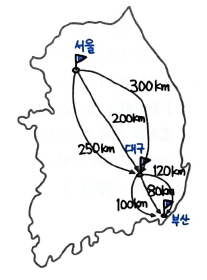
서울에서 부산까지 가는 최단 경로를 찾는 간단한 예를 들어보자.
그림에서 보듯이, 서울에서 대구까지 가는 경로는 3가지가 있으며, 부산까지도 마찬가지로 3가지 경로가 있다. 서울에서 부산까지 가는 최단 경로는 서울에서 대구까지 가는 최단 경로(200km)와 대구에서 부산까지 가는 최단 경로(80km)로 구성된다. 즉, 서울에서 부산까지 가는 최단 경로는 각각의 부분 문제인 1.서울에서 대구까지 가는 최단 경로 문제와 2.대구에서 부산까지 가는 최단 경로 문제의 해결 방법의 합이다. 따라서, 문제의 최적 해결 방법은 부분 문제에 대한 최적 해결 방법으로 구성된다.
이러한 구조를 최적 부분 구조라 하며, 이런 유형의 문제는 분할 정복으로 풀 수 있다. 또한 DP 또는 그리디로 접근해볼 수 있는 문제의 후보가 된다. 그러나, 만약 서울에서 부산까지 바로 연결되는 고속도로가 새롭게 개통되어 더 이상 대구를 거칠 필요가 없다면, 이 문제는 더 이상 최적 부분 구조가 아니다. 더는 분할 정복으로 풀 수 없으며, DP나 그리디로도 풀이할 수 없다.

중복된 하위 문제들

DP로 풀 수 있는 문제들과 다른 문제들의 결정적인 차이는 중복된 하위 문제들을 갖는다는 점이다.

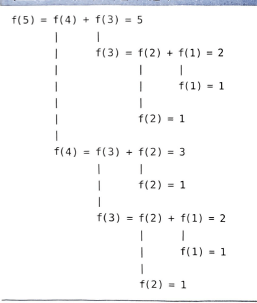
f(3) = f(2) + f(1) 이며, f(4) = f(3) + f(2) 이다. f(5) 또한 f(5) = f(4) + f(3) 이다. 이처럼, 피보나치 수열을 재귀로 풀면 반복적으로 동일한 하위 문제들이 발생한다. 이러한 중복된 하위 문제들을 풀이할 때, DP는 이미 계산한 결과를 저장해두었다가 재활용한다.
즉, 중복 문제가 발생하지 않는 병합 정렬은 분할 정복으로 분류되지만, 피보나치 수열을 풀이하는 알고리즘은 DP로 분류된다.

다이나믹 프로그래밍 방법론

지금까지 최적 부분 구조와 중복된 하위 문제들로 구성된 DP의 패러다임을 살펴봤고, 이제부터는 DP의 방법론을 알아볼 차례이다.
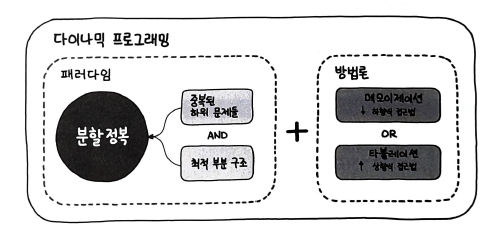
이 그림에서 방법론은 방식에 따라 크게 상향식과 하향식으로 나뉜다. 일반적으로 상향식을 타뷸레이션, 하향식을 메모이제이션이라고 부른다.

상향식(Bottom-Up)

더 작은 하위 문제부터 살펴본 다음, 작은 문제의 정답을 이용해 큰 문제의 정답을 풀어나간다.타뷸레이션(Tabulation) 이라 부르며, 일반적으로 이 방식만을 DP로 지칭하기도 한다.

하향식(Top-Down)

하위 문제에 대한 정답을 계산했는지 확인해가며 문제를 자연스러운 방식으로 풀어나간다. 이 방식을 특별히 메모이제이션(Memoization)이라 지칭한다.

피보나치 수열의 예제 코드를 보면서 상향식과 하향식의 차이를 살펴보자.

피보나치 수열 - 상향식

def fib(n) :
	dp[0] = 0
	dp[1] = 1

	for i in range(2, n + 1) :
		dp[i] = dp[i - 1] + dp[i - 2]
	return dp[n]

작은 하위 문제부터 차례대로 정답을 풀어나가며 큰 문제의 정답을 만든다. 이 방식을 타뷸레이션이라 하며, 이 방식만을 DP라 지칭하는 경우도 있다. 데이터를 테이블 형태로 만들면서(Tabulate) 문제를 풀이한다고 하여 타뷸레이션 방식이라고 부른다.

피보나치 수열 - 하향식

def fib(n) :
	if n <= 1 :
		return n

	if dp[n] :
		return dp[n]
	dp[n] = fib(n - 1) + fib(n - 2)
	return dp[n]

하향식 방법론은 하위 문제에 대한 정답을 계산했는지 확인해가며 문제를 자연스럽게 재귀로 풀어나간다. 기존 재귀 풀이와 거의 동일하면서도 이미 풀어봤는지 확인하여 재활용하는 효율적인 방식으로, 메모이제이션 방식이라고 부른다.

85. 피보나치 수

풀이 1. 재귀 구조 브루트 포스

def fib(N) :
	if N <= 1 :
		return N
	return fib(N - 1) + fib(N - 2)

888ms가 걸리는 느린 풀이이다. 최적화가 필요하다.

풀이 2. 메모이제이션

DP의 하향식 풀이로 정리한 것이 바로 이 문제의 메모이제이션 풀이이다.

class Solution :
	dp = collections.defaultdict(int)

	def fib(N) :
		if N <= 1:
			return N

		if self.dp[N] :
			return self.dp[N]
		self.dp[N] = self.fib(N - 1) + self.fib(N - 2)
		return self.dp[N]

원래의 브루트 포스 풀이와 유사하게 재귀로 계산해 나가지만, 이미 계산한 값은 저장해뒀다가 바로 리턴한다. 앞서 fib(5) 일때 15번의 연산을 진행하던 구조는 이 메모이제이션 풀이에서는 밑의 그림과 같이 9번의 연산만으로 풀이할 수 있게 된다. 한번 계산한 수는 더 이상 계산하지 않으므로, fib(2) 와 fib(3) 은 한 번만 계산하게 되어 매우 효율적이다.

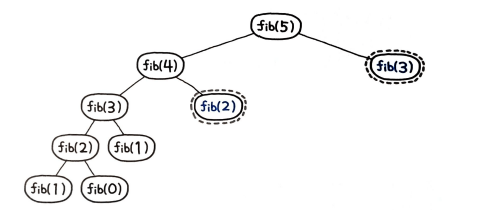
만약 시작이 fib(5)가 아니라 5보다 훨씬 더 큰 수라면 성능 차이는 훨씬 더 클 것이다.

풀이 3. 타뷸레이션

상향식 풀이의 코드는 다음과 같다.

class Solution:
	dp = collections.defaultdict(int)

	def fib(N) :
		self.dp[0] = 0
		self.dp[1] = 1

		for i in range(2, N + 1) :
			self.dp[i] = self.dp[i - 1] + self.dp[i - 2]
		return self.dp[N]

재귀를 사용하지 않고 반복으로 풀이하며, 작은 값부터 직접 계산하면서 타뷸레이션한다. 미리 계산을 해두는 것인데, 다른 복잡한 DP와는 달리 타뷸레이션이 일차원 선형 구조라 복잡하지 않고, 구조 자체도 단순해 이해가 쉬운 편이다. 메모이제이션과 마찬가지로 실행 속도도 당연히 빠르다.

풀이 4. 두 변수만 이용해 공간 절약

그런데 사실 앞서 풀이는 dp라는 딕셔너리(사실 단순 배열만 사용해도 충분하다)에 결과를 차곡차곡 담아 나갔지만 변수는 2개만 있어도 충분하다.

def fib(N) :
	x, y = 0, 1
	for i in range(N) :
		x, y = y, x + y
	return x

이 경우 앞서 풀이처럼 메소드 바깥에 클래스의 멤버 변수도 선언할 필요가 없기 때문에 코드는 훨씬 더 간결해진다. 공간 복잡도도 O(n) 에서 O(1)로 줄어든다. 시간 복잡도는 동일한 O(n) 이므로 매우 효율적이다.

풀이 5. 행렬

DP와는 관련없지만, n번째 피보차니 수를 O(log n) 번의 연산만으로 구할 수 있는 방법이 있다. 바로 넘파이 모듈을 사용하는 방식이다.

def fib(n) :
	M = np.martix([0, 1], [1, 1])
	vec = np.array ([[0], [1]])

	return np.matmul(M ** n, vec)[0]

풀이 2부터 4는 각각 28ms, 24ms, 24ms가 된다.

0-1 배낭 문제

DP의 또 다른 대표 문제 중 하나인 배낭 문제를 살펴보자. 짐을 쪼갤 수 없는 0-1 배낭 문제이다. 이 문제는 탐욕 선택 속성이 있는 문제가 아니며, 중복된 하위 문제들 속성을 갖고 있으므로, DP 풀이할 수 있다.
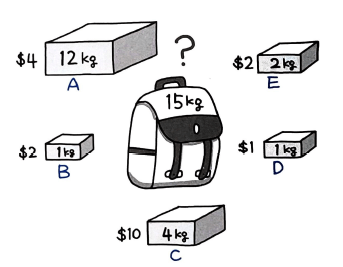
단가 순으로 그리디하게 배치해서 풀이했던 분할 기능 배낭 문제와 달리, 0-1 배낭 문제는 짐을 쪼갤 수 없다. 이 경우 모든 경우의 수를 계산해야 하며, 이렇게 모든 경우의 수를 계산하는 문제에서 DP는 위력을 발휘한다. 다음과 같이 풀이할 수 있따. 먼저, 입력값으로 짐을 정의하고 zero_one_knapsack() 풀이 함수를 호출한다.

cargo = [
	(4, 12), # (value, weight)
	(2, 1),
	(10, 4),
	(1, 1),
	(2, 2)
]

r = zero_one_knapsack(cargo)

zero_one_knapsack() 함수는 다음과 같이 정의한다.

def zero_one_knapsack(cargo) :
	capacity = 15
	pack = []

pack 이라는 리스트 변수에 6 X 16 행렬 형태의 중간 결과 테이블이 생성될 것이다. 즉, 이 테이블을 그자 그대로 타뷸레이션 하는 DP 풀이가 될 것이다. 테이블의 크기의 기준은 짐의 최대 개수 + 1, 배낭의 최대 용량 + 1 이렇게 6 X 16이며, 이 테이블 각각의 셀에는 그 위치까지의 짐의 개수와 배낭의 용량에 따른 최댓값이 담기게 된다.
실제로 어떤 값인지는 먼저 전체 코드부터 먼저 살펴본 이후에 다시 정리해보자.

def zero_one_knapsack(cargo) :
	capacity = 15
	pack = []

	for i in range(len(cargo) + 1) :
		pack.append([])
		for c in range(capacity + 1) :
			if i == 0 or c == 0:
				pack[i].append(0)

			elif cargo[i - 1][1] <= c :
				pack[i].append(
					max(
						cargo[i - 1][0] + pack[i - 1][c - cargo[i - 1][1]],
						pack[i - 1][c]
					))

			else :
				pack[i].append(pack[i - 1][c])

	return pack[-1][-1]

이 코드의 실행 결과로 pack에는 다음과 같은 표가 생성된다.

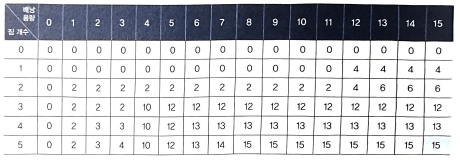
이 표에서 세로 축은 짐의 개수, 가로축은 배낭의 용량이다. 각각의 셀은 그 위치까지의 짐의 개수와 배낭의 용량에 따른 최댓값이다. 즉 짐이 4개가 있을 때는 차례대로 ($4, 12kg), ($2, 1kg), ($10, 4kg), ($1, 1kg) 일 것이고, 배냥의 용량이 4라면 4kg인 $10 짜리 짐 하나를 담는게 가장 이익이다. 따라서, 4 X 4 위치의 최댓값은 10이며 위의 표에서도 10인 것을 확인할 수 있다. 배낭의 용량이 5라면 1kg 인 $2 를 추가해 12가 될 수 있다. 마찬가지로 표에서도 12다. 이렇게 가장 마지막 위치인 5 X 15 까지 이동한 총 5개의 짐, 용량이 15인 배낭의 최댓값은 15이며, 이 문제의 정답은 15임을 확인할 수 있다.
이렇게 최아의 경우 O(2^n) 의 계산이 필요한 0-1 배낭 문제를 여기서는 타뷸레이션 방식으로 O(nW)(여기서 n은 짐의 개수, W는 배낭의 용량)에 잘 풀이해봤다.

86. 최대 서브 배열

합이 최대가 되는 연속 서브 배열을 찾아 합을 리턴하라.

• 입력 [-2, 1, -3, 4, -1, 2, 1, -5, 4]

• 출력 6

풀이 1. 메모이제이션

언뜻 투 포인터 문제인가 하는 생각이 들 수 있다. 그런데 생각해보면, 투 포인터로 풀이하기는 어렵다.
왼쪽 포인터가 -2이고, 오른쪽 포인터가 4라고 했을 때, 그 사잇값이 최대가 되기 위해서는 음수를 지나치는 방식으로 알고리즘을 구현해야 하는데, 연속된 서브 배열을 찾아야 하는 문제인 만큼 정렬을 할 수 없고, 그렇다면 다음 숫자가 뭐가 될지 모르는 상황에서 단순히 음수를 건너 뛰는 방식으로는 구현이 어렵다. 무엇보다 효율적으로 투 포인터로 풀이하기 위해서는 정렬이 필요하다.
그렇다면, 메모이제이션을 이용해 다음과 같은 결과를 만드는게 효과적이다.

#nums = [-2, 1, -3, 4, -1, 2, 1, -5, 4]
sums = [-2, 1, -2, 4, 3, 5, 6, 1, 5]

앞에서부터 계속 값을 계산하면서 누적 합을 계산한다. 이전 값을 계속 더해나가되, 0 이하가 되면 버린다. 어차피 최댓값을 찾는데 0 이하인 값은 굳이 서브 배열에 포함할 이유가 없기 때문이다.

def maxSubArray(nums) :
	sums = [nums[0]]
	for i in range(1, len(nums)) :
		sums.append(nums[i] + (sums[i - 1] if sums[i - 1] > 0 else 0))

	return max(sums)

이렇게 메모이제이션으로 값을 더해 나간 sums에서 최댓값을 추출하면 서브 배열의 최댓값을 찾을 수 있다. 여기서 sums라는 별도 변수를 사용했는데 가만히 살펴보면 추가 변수 없이도 충분히 처리가 가능할 것 같다. 전체 코드는 다음과 같다.

def maxSubArray(nums) :
	for i in range(1, len(nums)) :
		nums[i] += nums[i - 1] if nums[i - 1] > 0 else 0
	return max(nums)

기존 nums에 합을 함께 넣었다. 공간을 재활용하여 공간 복잡도를 없앴고, 풀이도 좀 더 깔끔해졌다.

풀이 2. 카데인 알고리즘

제이 카데인이 O(n)에 풀이가 가능하도록 고안한 카데인 알고리즘 이라는 해법도 존재한다. 당시 그는 최대 서브 배열을 찾기 위해 어디서 시작되는지를 찾는 문제 O(n^2) 풀이에서 각 단계마다 최댓값을 담아 어디서 끝나는지를 찾는 문제 O(n) 풀이로 치환해서 풀이했다. 전체 풀이 코드는 다음과 같다.

def maxSubArray(nums) :
	best_sum = -sys.maxsize
	current_sum = 0
	for num in nums :
		current_sum = max(num, current_sum + num)
		best_sum = max(best_sum, current_sum)

	return best_sum

이전 풀이에서는 매번 계산해서 넣기만 하고 마지막에 max()를 전체 계산해서 가져오게 했지만, 당시 제이 카데인은 이런 형태로 매번 best_sum 을 계산하게 했다. 하지만 사실상 동일한 코드로 볼 수 있으며, 속도 또한 양쪽 모두 동일하다.

87. 계단 오르기

정상에 도달하기 위해 n 계단을 올라야 한다. 매번 각각 1계단 또는 2계단씩 오를 수 있다면 정상에 도달하기 위한 방법은 몇 가지 경로가 되는지 계산하라.

• 입력
  3
• 출력
  3
• 설명
  정상에 오르기 위한 방법은 3가지 경로가 있다.
  a. 1계단 + 1계단 + 1계단
  b. 1계단 + 2계단
  c. 2계단 + 1계단

풀이 1. 재귀 구조 브루트 포스

언뜻 생각해보면 모든 경우의 수를 다 찾아야해서 상당히 풀기 어려워 보인다. 그러나 다음과 같이 경우의 수를 하나씩 그려보면 기본적으로 피보나치 수와 동일한 유형의 문제라는 것을 알 수 있다. 다만, 방법과 형식이 달라 연상하기 어려울 뿐이며, 동일한 방식으로 풀이할 수 있다.
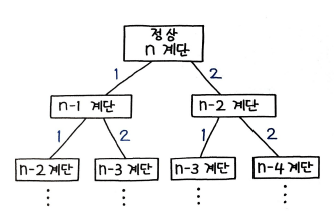
이처럼 새로운 유형의 문제를 피보나치 수열 같은 기존의 유명한 문제와 연결해 풀이하는 방법은 문제 해결에 매우 좋은 방법이다. 피보나치 수열과 완전히 동일한 풀이로 다음과 같이 간단한 재귀로 풀 수 있다.

def climbStairs(n) :
	if n == 1 :
		return 1
	if n == 2 :
		return 2
	return climbStairs(n - 1) + climbStairs(n - 2)

그러나 타임아웃이 발생하므로, 메모이제이션을 적용해야 한다.

풀이 2. 메모이제이션

class Solution :
	dp = collections.defaultdict(int)

	def climbStairs(self, n) :
		if n <= 2 :
			return n

		if self.dp[n] :
			return self.dp[n]

		self.dp[n] = self.climbStairs(n - 1) + self.climbStairs(n - 2)
		return self.dp[n]

40ms가 걸린다. 기존의 풀이와 연결해 풀이하는 연습을 꾸준히 해보자.

88. 집 도둑

어느 집에서는 돈을 훔쳐올 수 있지만 경보 시스템 때문에 바로 옆집은 훔칠 수 없고 한 칸 이상 떨어진 집만 가능하다. 각 집에는 훔칠 수 있는 돈의 액수가 입력값으로 표기되어 있다. 훔칠 수 있는 가장 큰 금액을 출력하라.

• 입력
  [1, 2, 3, 1]
• 출력
  4
• 설명 첫 번째 집과 세 번째 집을 훔치면 4가 최대 금액이다.

풀이 1. 재귀 구조 브루트 포스

이제 이런 유형의 문제를 보면 바로 DP를 떠올릴 수 있을 것 같다. 바로 옆집은 훔칠 수 없으니, 현재 집과 옆집 숫자 중의 최댓값을 구하고, 한 집 건넛집까지의 최댓값과 현재 집의 숫자값과의 합을 구해서 두 수 중 더 높은 값이 정답이 된다. 이렇게 하면 역시 피보나치 수열과 거의 유사한 형태로, 다음과 같이 간단한 재귀로 풀 수 있다.

nums: List[int]
def rob(i: int) -> int:
	...
	return max(rob(i - 1), rob(i - 2) + nums[i])

브루트 포스로 구현해보면 다음과 같다. 앞서 rob() 함수를 중첩 함수로 처리하고, 문제 풀이 함수와 이름이 겹치므로 밑줄을 추가해 내부 함수라는 의미를 부여해봤다.

def rob(nums) :
	def _rob(i) :
		if i < 0 :
			return 0
		return max(_rob(i - 1), _rob(i - 2) + nums[i])
	return _rob(len(nums) - 1)

하지만 역시 타임아웃으로 풀리지 않는다. 집이 10채, 즉 len(nums)가 10이라면 탐색 횟수가 287회나 된다.

풀이 2. 타뷸레이션

이미 계산한 값은 dp에 저장하고 두 번 이상 계산하지 않는다.

dp[0], dp[1] = nums[0], max(nums[0], nums[1])
for i in range(2, len(nums)) :
	dp[i] = max(dp[i - 1], dp[i - 2] + nums[i])

변수명은 dp이며 여기서는 메모이제이션이 아닌 타뷸레이션으로 풀이했다. 아무래도 재귀로 구현하는 메모이제이션보다 순회 방식인 타뷸레이션이 좀 더 직관적이여서 이해하기 쉬운 편이다. 결과는 파이썬의 해시 테이블인 딕셔너리에 넣을 것인데, 원래 딕셔너리는 입력 순서가 유지되지 않았으나, 파이썬 3.7+ 부터는 입력 순서가 유지된다. 하지만 여기서는 파이썬의 낮은 버전에서도 순서가 유지될 수 있도록 명시적으로 collections.OrderedDict() 로 선언해 풀이해본다.
이제 가장 마지막 값을 추출하기 위해 popitem()을 사용한다. 리스트의 pop()과 동일한 역할을 하는데, 딕셔너리에도 pop()이 있지만 반드시 키를 지정해야 하고 해당 키의 아이템을 추출하는 역할을 한다. 딕셔너리에서 가장 마지막 아이템을 추출하기 위해서는 이처럼 popitem()을 사용한다.

dp = collections.OrderedDict()
...
return dp.popitem()[1]

이제 전체 코드는 다음과 같다.

def rob(nums) :
	if not nums :
		return 0
	if len(nums) <= 2 :
		return max(nums)

	dp = collections.OrderedDict()
	dp[0], dp[1] = nums[0], max(nums[0], nums[1])
	for i in range(2, len(nums)) :
		dp[i] = max(dp[i - 1], dp[i - 2] + nums[i])
	return dp.popitem()[1]

28ms가 걸린다.

딕셔너리 입력 순서 유지

파이썬 3.7부터는 collections.OrderedDict가 아니더라도, 다음과 같은 형태로 맨 마지막 값을 추출할 수 있다.

list(a.keys())[-1]

그러나 원래 해시 테이블은 입력 순서가 유지되지 않는다. 많이 실수하는 부분이고 오죽하면 C++ 에서는 해시 테이블 자료형의 이름이 정렬되지 않은 맵(std::unordered_map) 일 정도이니 말이다.
3.6 이하의 버전에서는 위의 코드가 오작동할 수 있으므로, 구 버전에도 동작하는 collections.OrderedDict라는 좋은 자료형을 활용하자.