분할 정복

분할 정복은 다중 분기 재귀를 기반으로 하는 알고리즘 디자인 패러다임을 말한다.

직접 해결할 수 있을 정도로 간단한 문제가 될 때까지 문제를 재귀적으로 쪼개나간 다음, 그 하위 문제의 결과들을 조합하여 원래 문제의 결과로 만들어내는 방식이다. 대표적으로는 병합 정렬을 예시로 들 수 있다.

분할 : 문제를 동일한 유형의 여러 하위 문제로 나눈다.
정복 : 가장 작은 단위의 하위 문제를 해결하여 정복한다.
조합 : 하위 문제에 대한 결과를 원래 문제에 대한 결과로 조합한다.

말 그대로 문제를 분할해서 정복한 다음, 정답을 조합해 나간다는 의미를 지닌다. 정의에서도 재귀가 언급되어 있는 것처럼 분할 정복은 재귀를 활용하는 대표적인 알고리즘이기도 하다. 수도코드로 표현해보면 다음과 같은 형태가 된다.

function F(x) :
	if F(x)가 간단 then :
		return F(x)를 계산한 값 # 2. 정복

	else :
		x를 x1, x2로 분할 # 1. 분할
		F(x1)과 F(x2)를 재귀 호출
		return F(x1)과 F(x2)로 F(x)를 구한 값 # 3. 조합

이 같은 알고리즘 디자인 패러다임은 중급 이상의 코딩 테스트 문제로 빈번히 출제되며 23장에서 다시 한번 살펴보게 될 최적 부분 구조 를 풀이하는 매우 중요한 기법 중 하나이므로 잘 숙지해 둘 필요가 있다.

83. 과반수 엘리먼트

과반수를 차지하는(절반을 차지하는) 엘리먼트를 출력하라.

풀이 1. 브루트 포스로 과반수 비교

앞에서부터 하나씩 과반수를 넘는지 일일이 체크하다가 과반수를 넘으면 바로 정답으로 처리하는 방법이다.

def majorityElement(self, nums) :
	for num in nums :
		if nums.count(num) > len(nums) // 2:
			return num

하지만 타임아웃이 발생한다.

// 연산자

// 연사자는 결과가 실수일 때 내림 처리를 하고 동일한 자료형을 리턴해주는 파이썬 특유의 편리한 연산자다.

>>> 5 / 3
1.6666666666666667
>>> 5 // 3
1
>>> 5.0 // 3
1.0
>>> 5 // 3.0
1.0
>>> 5.0 // 3.0
1.0
>>> math.floor(5/3)
1

풀이 2. 다이나믹 프로그래밍

def majorityElement(nums) :
	counts = collections.defaultdict(int)
	for num in nums :
		if counts[num] == 0 :
			counts[num] = nums.count(num)

		if counts[num] > len(nums) // 2 :
			return num

nums.count() 로 한 번 카운트를 계산한 값을 저장해서 재활용했다. 만약 계산되지 않았던 값이 들어온다면 항상 0이 될 것이고, 그 때만 카운트를 계산하게 될 것이다. 이 풀이는 메모이제이션 을 이용한 DP 풀이의 에시이다.

`풀이 3. 분할 정복`

병합 정렬과 매우 유사한 방식으로 풀이할 수 있다. 쪼갠 다음 정렬해서 각각의 엘리멘트를 전부 리턴하는 병합 정렬과 매우 유사한 방식으로 풀이할 수 있다. 쪼갠 다음 정렬해서 각각의 엘리먼트를 전부 리턴하는 병합정렬과 달리 여기서는 과반수 후보군에 해당하는 엘리멘트만 리턴 하면서 밑 그림과 같이 계속 위로 올려주면, 즉 백트래킹 하면 최종적으로 정답이 남게 된다.

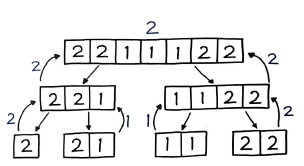
코드는 다음과 같은 식이다.

def majorityElement(self, nums) :
	...

	a = self.majorityElement(nums[:len(nums) // 2])
	b = self.majorityElement(nums[len(nums) // 2:])

이런식으로 먼저 분할을 시도한다. a와 b는 각각 최소 단위로 쪼개질 것이다. 물론 그렇게 하기 위해서는 상단에 끊어서 리턴해주는 부분이 필요하다.

def majorityElement(self, nums) :
	if not nums :
		return None
	if len(nums) == 1 :
		return nums[0]
	a = self.majorityElement(nums[:len(nums) // 2])
	b = self.majorityElement(nums[len(nums) // 2:])

이제 이렇게 리턴해주면, 최소 단위로 쪼개질 때 해당하는 값을 리턴하게 될 것이다. 마지막으로 백트래킹될 때 처리하는 부분, 즉 정복에 해당하는 부분을 다음과 같이 구현해보자.

return [b, a][nums.count(a) > len(nums) // 2]

a가 만약 현재 분할된 리스트 nums에서 과반수를 차지한다면 해당 인덱스는 1이 될 것이고, [b, a][1] 이 되어 a를 리턴할 것이다. 즉 과반수인 엘리먼트를 리턴한다.
이외에는 b를 리턴한다.

def majorityElement(self, nums) :
	if not nums :
		return None
	if len(nums) == 1 :
		return nums[0]

	half = len(nums) // 2
	a = self.majorityElement(nums[:half])
	b = self.majorityElement(nums[half:])

	return [b, a][nums.count(a) > half]

half 변수에 len(nums) // 2 를 저장해두면 10% 가량 속도를 더 높일 수 있다. 재귀 풀이의 특성상 DP 나 다른 방식에 비해서는 속도가 다소 느린 편이다.

풀이 4. 파이썬 다운 방식

이제 파이썬다운 방식으로도 풀이해보자.

def majorityElement(self, nums) :
	return sorted(nums)[len(nums) // 2]

정렬하여 가운데를 지정하면 반드시 과반수 이상인 엘리먼트 일 것이다. 매우 직관적이며 쉬운 알고리즘이다.

84. 괄호를 삽입하는 여러 가지 방법

슷자와 연산자를 입력받아 가능한 모든 조합의 결과를 출력하라.

입력
“2-1-1”
출력
[0, 2]
설명
((2-1)-1) = 0
(2-(1-1)) = 2
입력
“2x3-4x5”
출력
[-34, -14, -10, -10, 10]
설명
((2x(3-(4x5))) = -34
((2x((3-4)x5)) = -14
((2x(3-4))x5) = -10
((2x3)-(4x5)) = -10
(((2x3)-4)x5) = 10

풀이 1. 분할 정복을 이용한 다양한 조합

괄호를 어디에 추가하느냐에 따라 다양한 조합이 가능하다.

def diffWaysToCompute(self, input) :
	...
	results = []
	for index, value in enumerate(input) :
		if value in "-+*" :
			left = self.diffWaysToCompute(input[:index])
			right = self.diffWaysToCompute(input[index + 1:])

			results.extend(compute(left, right, value))
	return results

연산자를 기준으로 left, right를 계속 분할하고, 분할된 값은 compute() 함수로 계산한 결과를 extend()로 확장한다.

def diffWaysToCompute(self, input) :
	...
	if input.isdigit() :
		return [int(input)]

분할 결과를 리턴받으려면 이처럼 input이 숫자형일 때 리턴하게 한다. 이렇게 하면 분할의 결과가 최종적으로 숫자형인 타입을 재귀의 최종 결과로 리턴하게 될 것이다. 이제 게산하는 부분은 다음과 같다.

def compute(left, right, op) :
	results = []
	for l in left :
		for r in right :
			results.append(eval(str(l) + op + str(r)))
	return results

위의 코드를 합친 결과는 다음과 같다.

def diffWaysToCompute(self, input) :
	def compute(left, right, op) :
		results = []
		for l in left :
			for r in right :
				results.append(eval(str(l) + op + str(r)))
		return results

	if input.isdigit() :
		return [int(input)]

	results = []
	for index, value in enumerate(input) :
		if value in "-+*" :
			left = self.diffWaysToCompute(input[:index])
			right = self.diffWaysToCompute(input[index + 1:])

			results.extend(compute(left, right, value))
	return results

append() vs extend()

>>> a = [1, 2, 3]
>>> b = [4, 5]
>>> a.append(b)
>>> a
[1, 2, 3, [4, 5]]

리스트에 또 다른 리스트를 삽입할 때 append()는 이처럼 리스트 전체를 또 다른 엘리멘트로 처리한다.

>>> a = [1, 2, 3]
>>> b = [4, 5]
>>> a.extend(b)
>>> a
[1, 2, 3, 4, 5]

반면 extend()는 삽입 대상의 리스트를 풀어서 각각의 엘리멘트로 확장(Extend) 해 삽입한다. 앞서 풀이에서는 삽입 대상이 복수형이 될 수도 있기 때문에 풀어서 삽입하는 extend() 를 사용했다.

분할 정복
83. 과반수 엘리먼트
84. 괄호를 삽입하는 여러 가지 방법
- 풀이 1. 분할 정복을 이용한 다양한 조합
  - append() vs extend()