각 간선의
가중치 합이 최소가 되는 두 정점(또는 노드) 사이의 경로를 찾는 문제
정점은 교차로에 해당하고 간선은 길에 해당한다. 가중치는 거리나 시간과 같은 이동 비용에 해당한다.
여러 개의 최단 경로 알고리즘 중, 가장 유명한 것은 다익스트라 알고리즘일 것이다.
다익스트라 알고리즘은 항상 노드 주변의 최단 경로만을 택하는 대표적인 그리디 알고리즘 중 하나로, 단순할 뿐만 아니라 실행 속도 또한 빠르다. 다익스트라는 노드 주변을 탐색할 떄 BFS를 이용하는 대표적인 알고리즘이기도 하다.
DFS는 한 사람이 미로를 찾아 헤매는 과정과 비슷한 반면, BFS는 여러명의 사람이 각기 서로 다른 갈릴김로 흩어져서 길을 찾는 것과 비슷하다.
40. 네트워크 딜레이 타임
K 부터 출발해 모든 노드가 신호를 받을 수 있는 시간을 계산하라. 불가능할 경우 -1을 리턴한다. 입력값 (u, v, w)는 각각 출발지, 도착지, 소요 시간으로 구성되며, 전체 노드의 개수는 N으로 입력받는다.
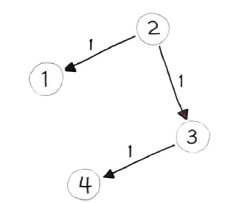
- 입력
times = [[2,1,1],[2,3,1],[3,4,1]], N = 4, K = 2
풀이 1. 다익스트라 알고리즘 구현
이 문제에서는 다음과 같은 2가지 사항을 판별해야 한다.
- 모든 노드가 신호를 받는 데 걸리는 시간
- 모든 노드에 도달할 수 있는지 여부
다익스트라 알고리즘을 좀 더 효율적으로 구현하기 위해 우선순위 큐 방식을 적용한다. 파이썬에서 우선순위 큐를 최소 힙으로 구현한 모듈인 heapq를 사용하는 형태로 구현해본다. 다음은 다익스트라 알고리즘의 수도코드이다.
function Dijkstra(Graph, source) :
dist[source] ← 0
create vertex priority queue Q
for each vertex v in Graph :
if v ≠ source
dist[v] ← INFINITY
prev[v] ← UNDEFINED
Q.add_with_priority(v, dist[v])
while Q is not empty :
u ← Q.extract_min()
for each neighbor v of u :
alt ← dist[u] + length(u, v)
if alt < dist[v] :
dist[v] ← alt
prev[v] ← u
Q.decrease_priority(v, alt)
return dist, prev그래프에서 각 정점과 거리를 우선순위 큐에 삽입하는 부분 Q.add_with_priority(v, dist[v]), 그리고 우선순위 큐에서 최소 값 추출(u ← Q.extract_min())을 통해 이웃을 살펴보는 (for each neighbor v of u) 수도코드를 확인할 수 있다. 이제 이 수도코드 알고리즘을 실제로 실행 가능한 파이썬 코드로 구현해보자.
graph = collections.defaultdict(list)
for u, v, w in times :
graph[u].append((v, w))먼저 그래프를 인접 리스트로 표현하는 딕셔너리부터 만들어준다.
다음은 우선순위 큐를 위한 큐 변수를 정의한다.
Q = [(0, K)]
dist = collections.defaultdict(int)큐 변수 Q는 ‘(소요 시간, 정점)’ 구조로 구성한다. 수도코드에는 큐에 add_with_priority(), decrease_priority(), extract_min(), 3번의 연산을 내리도록 구현되어 있다. 여기서 add_with_priority() 와 extract_min() 은 문제없지만, decrease_priority 가 문제다. heapq 모듈은 우선순위 업데이트를 지원하지 않는다.
따라서, decrease_priority() 연산이 핌요 없도록 다음과 같이 알고리즘을 살짝 변경해야 한다.
while Q :
time, node = heapq.heappop(Q)
if node not in dist :
dist[node] = time
for v, w in graph[node] :
alt = time + w
heapq.heappush(Q, (alt, v))마지막으로 모든 노드에 도달할 수 있는지 여부를 다음과 같이 판별한다.
if len(dist) == N :
return max(dist.values())
return -1전체 코드를 정리하면 다음과 같다.
def networkDelayTime(times, N, K) :
graph = collections.defaultdict(list)
# 그래프 인접 리스트 구성
for u, v, w in times :
graph[u].append((v, w))
# 큐 변수 : [(소요 시간, 정점)]
Q = [(0, K)]
dist = collections.defaultdict(int)
# 우선순위 큐 최솟값 기준으로 정점까지 최단 경로 삽입
while Q :
time, node = heapq.heappop(Q)
if node not in dist :
dist[node] = time
for v, w in graph[node] :
alt = time + w
heapq.heappush(Q, (alt, v))
# 모든 노드의 최단 경로 존재 여부 판별
if len(dist) == N :
return max(dist.values())
return -141. K 경유지 내 가장 저렴한 항공권
시작점에서 도착점까지의 가장 저렴한 가격을 계산하되, K개의 경유지 이내에 도착하는 가격을 리턴하라.
풀이 1. 다익스트라 알고리즘 응용
가격을 시간이라고 가정한다면 최단 시간을 계산하는 경로는 앞서 다익스트라 알고리즘으로 동일하게 구현할 수 있다. 다만, 여기에는 한 가지 제약사하잉 추가되었는지 K개의 경유지 이내에 도착해야 한다는 점이다. 따라서, 다익스트라 알고리즘의 구현을 위해 우선순위 큐에 추가할 때 K 이내일 때만 경로를 추가하여 K를 넘어서는 경로는 더 이상 탐색되지 않게 하면 된다.
전체거리를 보관할 필요가 없기 때문에 40번 문제 풀이의 dist 딕셔너리는 삭제해도 된다. 도착점까지의 최단 경로만 계산하면 된다. 전체 경로의 개수도 체크할 필요가 없다.
최종코드는 다음과 같다.
def findCheapestPrice(flights, src, dst, K) :
graph = collections.defaultdict(list)
# 그래프 인접 리스트 구성
for u, v, w in flights :
graph[u].append((v, w))
# 큐 변수 : [(가격, 정점, 남은 가능 경유지 수)]
Q = [(0, src, K)]
# 우선순위 큐 최솟값으로 기준으로 도착점까지 최소 비용 판별
while Q :
price, node, k = heapq.heappop(Q)
if node == dst :
return price
if k >= 0 :
for v, w in graph[node] :
alt = price + w
heapq.heappush(Q, (alt, v, k-1))