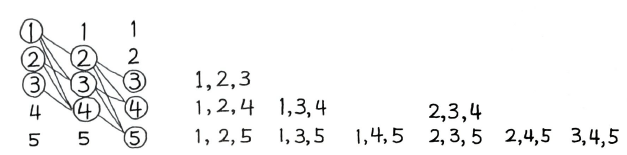그래프

객체의 일부 쌍들이 ‘연관되어’ 있는 객체 집합 구조

오일러 경로

모든 간선을 한 번씩 방문하는 경로

해밀턴 경로

각 정점을 한 번씩 방문하는 무향 또는 유향 그래프 경로

오일러 경로는 간선을 기준으로 하고, 해밀턴 경로는 정점을 기준으로 한다는게 차이점이다.
원래의 출발점으로 돌아오는 경로는 특별히 해밀턴 순환이라 한다. 이중에서도 특히 최단 거리를 찾는 문제는 알고리즘 분야에서는 외판원 문제 라고 한다.

NP 복잡도

NP는 Non-deterministic Polynomial의 약자로, 다항 시간에 풀 수 있는 판정 문제의 집합이다.
헷갈릴 수 있는 부분은 해밀턴 경로 문제와 외판원 문제의 NP 문제가 다르다는 점이다.

• 해밀턴 경로 : 한 번만 방문하는 경로
• 해밀턴 순환 : 한 번만 방문하여 출발지로 돌아오는 경로
• 외판원 문제 : 한 번만 방문하여 출발지로 돌아오는 경로 중 가장 짧은 경로

위의 세 문제를 보면 해밀턴 경로 > 해밀턴 순환 > 외판원 문제 의 포함 관계를 이룹니다.

그래프 순회

그래프 탐색이라고도 하며, 그랲의 각 정점을 방문하는 과정을 말한다.

그래프의 각 정점을 방문하는 그래프 순회에는 크게 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)이 있다.
일반적으로 BFS보다 DFS가 더 널리 쓰인다.
DFS는 주로 스택으로 구현하거나 재귀로 구현하며, 이후에도 살펴볼 백트래킹을 통해 뛰어난 효용을 보인다. 반면, BFS는 주로 큐로 구현하며 그래프의 최단 경로를 구하는 문제 등에 사용된다.
그래프를 표현하는 방법에는 크게 인접 행렬과 인접 리스트가 있다.

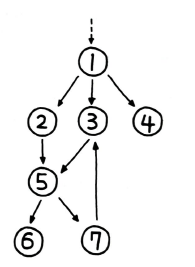
파이썬의 딕셔너리 자료형으로 다음과 같이 나타낼 수 있다.

graph = {
	1: [2, 3, 4],
	2: [5],
	3: [5],
	4: [],
	5: [6, 7],
	6: [],
	7: [3]
}

이 딕셔너리를 입력값으로 해서 각각 DFS, BFS를 구현해보자.

DFS(깊이 우선 탐색)

일반적으로 스택으로 구현하며, 재귀를 이요하면 좀 더 간단하게 구현할 수 있다.
코딩 테스트 시에도 재귀 구현이 더 선호되는 편이다.

재귀 구조로 구현

위키피디아에 제세된 수도코드는 밑 코드와 같다.

DFS(G, v) :
	label v as discovered
	for all directed edges from v to w that are in G.adjacentEdges(v) do
		if vertex w is not labeled as discovered then
			recursively call DFS(G, w)

정점 v의 모든 인접 유향(Directed) 간선들을 반복하라고 표기되어 있다.
이 알고리즘을 파이썬 코드로 구현해보면 다음과 같다.

def recursive_df(v, discovered = []) :
	discovered.append(v)
	for w in graph(v) :
		if w not in discovered :
			discovered = recursive_df(w, discovered)
	return discovered

discorvered는 방문한 정점들을 저장하는 리스트이다. 이걸 누적된 결과로 만들기 위해 리턴하는 형태만 받아오도록 처리했을 뿐 다른 부분들은 변수명까지 동일하게 수도코드와 맞춰서 작성한 결과이다. 그림으로 표현하면 다음과 같다.

스택을 이용한 반복 구조로 구현

이번에는 스택을 이용한 반복 결과로 DFS를 구현했다.

def iterative_dfs(start_v) :
	discorvered = []
	stack = [start_v]
	while stack :
		v = stack.pop()
		if v not in discovered :
			discovered.append(v)
			for w in graph[v] :
				stack.append(w)
	return discovered

이와 같은 반복 구현은 재귀 구현에 비해 더 직관적이고 실행 속도 또한 더 빠르다.
방문순서는 [1, 4, 3, 5, 7, 6, 2] 이다. 스택으로 구현하다 보니 가장 마지막에 삽입된 노드부터 꺼내서 반복하게 되고 이 경우 인접 노드에서 가장 최근에 담긴 노드, 즉 가장 마지막부터 방문하기 때문이다.

BFS(너비 우선 탐색)

BFS는 DFS보다 쓰임새는 적지만, 최단 경로를 찾는 다익스트라 알고리즘 등에 매우 유용하게 쓰인다. 먼저 BFS를 반복 구조로 구현해보자.

큐를 이용한 반복 구조로 구현

모든 인접 간성을 추출하고 도착점인 정점을 큐에 삽입하는 원리이다. 파이썬 코드로 구현하면 다음과 같다.

def iterative_bfs(start_v) :
	discovered = [start_v]
	queue = [start_v]
	while queue :
		v = queue.pop(0)
		for w in graph[v] :
			if w not in discovered :
				discovered.append(w)
				queue.append(w)
	return discovered

이와 같이 구현하면 방문 순서는 [1, 2, 3, 4, 5, 6, 7] 이 된다.
BFS의 경우 단계별 차례인 숫자 순으로 실행됬으며, 1부터 순서대로 각각의 인접 노드를 우선적으로 방문하는 식으로 실행된다.

재귀 구현 불가

BFS는 DFS와 달리 재귀 구조로 구현할 수 없다. BFS는 큐를 이용해 구현하는데, 재귀 구조는 함수의 호출과 복귀를 이용해 구현하는데, 이는 스택을 이용하는 것과 같다. 따라서 BFS는 반복 구조로만 구현할 수 있다.

백트래킹

해켤책에 대한 후보를 구축해 나아가다 가능성이 없다고 판단되는 즉시 후보를 포기(백트랙)

백트래킹은 DFS와 같은 방식으로 탐색하는 모든 방법을 뜻하며, DFS는 백트래킹의 골격을 이루는 알고리즘이라고 할 수 있다. 백트래킹은 주로 재귀로 구현하며, 알고리즘마다 DFS의 변형이 조금씩 일어나지만 기본적으로 모두 DFS의 범주 에 속한다.
백트래킹은 운이 좋으면 시행착오를 ㄷ러 거치고 목적이에 도착할 수 있지만 최악의 경우에는 모든 경우를 다 거친 다음에 도착할 수 있다. 이 때문에 브루트 포스와 유사하다. 하지만 한번 방문 후 가능성이 없는 경우에는 즉시 후보를 포기한다는 점에서 매번 같은 경로를 방문하는 브루트 포스보다는 훨씬 더 우아한 방식이라 할 수 있다.
위의 사진을 트리의 가지치기(Pruning)라고 하며, 불필요한 부분을 일찍 포기한다면 탐색을 최적화 할 수 있다.

제약 충족 문제

수많은 제약 조건을 충족하는 상태를 찾아내는 수학 문제

백트래킹은 제약 충족 문제(Constraint Satisfaction Problems 이하 CSP)를 풀이하는데 필수적인 알고리즘이다. 앞서 살펴본 가지치기를 통해 제약 충족 문제를 최적화 하기 때문이다.
예시로는 스토쿠, 십자말 풀이, N-Queen 문제 등이 있다.

32. 섬의 개수

1을 육지로, 0을 물로 가정한 2D 그리드 맵이 주어졌을 때, 섬의 개수를 계산하라. (연결된 1의 덩어리 개수를 구하라)

풀이 1. DFS로 그래프 탐색

반드시 그래프 모양이 아니더라도 그래프형으로 변환해서 풀이할 수 있음을 확인해보는 좋은 문제다. 네 방향으로 DFS 재귀를 이용해 탐색을 끝마치면 1이 증가하는 형태로 육지의 개수를 파악할 수 있다.

for i in range(len(grid)) :
	for j in range(len(grid[0])) :
		if grid[i][j] == '1' :
			self.dfs(grid, i, j)

육지를 발견하면 그때부터 self.dfs() 를 호출해 탐색 시작.

def dfs(self, grid, i, j) :
	# 더 이상 땅이 아닌 경우 종료
	if i < 0 or i >= len(grid) or \
		j < 0 or j >= len(grid[0]) or \
		grid[i][j] != '1' :
		return

	grid[i][j] = '0' # 가지치기

	# 동서남북 탐색
	self.dfs(grid, i + 1, j)
	self.dfs(grid, i - 1, j)
	self.dfs(grid, i, j + 1)
	self.dfs(grid, i, j - 1)

함수 상단에는 유직가 아닌 곳은 return 으로 종료 조건을 설정해둔다. 육지(1) 를 더 이상 육지가 아닌 곳으로 설정해야 다시 계산하는 경우가 생기지 않는다. 일종의 가지치기라 할 수 있다.
간혹, 또 다른 행렬을 생성해 그곳에 방문했던 경로를 저장하는 형태로 풀이가 가능하긴 한데 그렇게 하면 공간 복잡도가 O(n) 이 되기 때문에 공간의 활용이 비효율적이다. dfs() 함수를 빠져 나온 후에는 해당 위치에서 탐색할 수 있는 모든 육지를 탐색한 것 이므로, 카운트를 1 증가시킨다. 이제 입력값이 비어 있는 경우에 대해 예외 처리를 포함한 전체 코드는 다음과 같다.

class Solution(self, grid, i, j) :
	def dfs(self, grid, i, j) :
		# 더 이상 땅이 아닌 경우 종료
		if i < 0 or i >= len(grid) or \
			j < 0 or j >= len(grid[0]) or \
			grid[i][j] != '1' :
			return

		grid[i][j] = '0' # 가지치기

		# 동서남북 탐색
		self.dfs(grid, i + 1, j)
		self.dfs(grid, i - 1, j)
		self.dfs(grid, i, j + 1)
		self.dfs(grid, i, j - 1)

	def numIslands(self, grid) :
		count = 0

		for i in range(len(grid)) :
			for j in range(len(grid[0])) :
				if grid[i][j] == '1' :
					self.dfs(grid, i, j)
					count += 1

		return count

여기서, grid를 계속해서 넘기는 부분을 파이썬의 중첩함수 기능을 활용하여 다음과 같이 표현할 수 있다.

def numIslands(self, grid) :
	def def(i, j) :
		# 더 이상 땅이 아닌 경우 종료
		if i < 0 or i >= len(grid) or \
			j < 0 or j >= len(grid[0]) or \
			grid[i][j] != '1' :
				return

		grid[i][j] = 0

		# 동서남북 탐색
		dfs(i + 1, j)
		dfs(i - 1, j)
		dfs(i, j + 1)
		dfs(i, j - 1)
	
	count = 0
	for i in range(len(grid)) :
		for j in range(len(grid[0])) :
			if grid[i][j] == '1' :
				dfs(i, j)
				# 모든 육지 탐색 후 카운트 1 증가
				count += 1

numIslands() 함수 내에 dfs() 함수 전체가 중첩 함수로 들어갔다. 중첩 함수는 부모 함수에서 선언한 변수도 유효한 범위 내에서 사용가능하다.

중첩함수

함수 내에 위치한 또 다른 함수로, 바깥에 위치한 함수들과 달리 부모 함수의 변수를 자유롭게 읽을 수 있다는 장점이 있다. 중첩 함수는 부모 함수의 변수를 자유롭게 읽을 수 있지만, 부모 함수의 변수를 변경할 수는 없다. 중첩 함수는 부모 함수의 변수를 변경할 수 없기 때문에 부모 함수의 변수를 변경하고 싶다면 nonlocal 키워드를 사용해야 한다.

def outer_function(t) :
	text = t
	print(id(text), text)
	
	def inner_function1() :
		text = 'World!'
		print(id(text), text)
	
	def inner_function2() :
		print(id(text), text)

	inner_function1()
	inner_function2()

outer_function('Hello!')

위 코드를 실행하면 다음과 같은 결과가 나온다.

140711000000000 Hello!
147211000000123 World!
140711000000000 Hello!

inner 함수에서 값을 재할당해줘도 부모 함수에서는 반영이 되지 않으므로 주의가 필요하다.

33. 전화 번호 문자 조합

2에서 9까지 숫자가 주어졌을 때 전화번호로 조합 가능한 모든 문자를 리턴하라.

풀이 1. 모든 조합 탐색

이 문제를 전체를 탐색하여 풀이가 가능하다. 각 자릿수에 해당하는 키판 배열을 DFS로 탐색하면 결과가 완성된다.

digits = "23"
path = ""

def letterCombinations(digits) :
	def dfs(index, path) :
		# 끝까지 탐색하면 백트래킹
		if len(path) == len(digits) :
			result.append(path)
			return 

		# 입력값 자릿수 단위 반복
		for i in range(index, len(digits)) :
			# 키패드 배열의 문자열 단위 반복
			for j in dic[digits[i]] :
				dfs(i + 1, path + j)

	# 예외처리
	if not digits : 
		return []

	dic = { "2": "abc", "3" : "def", "4": "ghi", "5": "jkl",
					"6": "mno", "7": "pqrs", "8": "tuv", "9": "wxyz"}
	result = []
	dfs(0, "")

return result

다음 그림과 같이 DFS를 통해 모든 조합을 탐색한다.

34. 순열

서로 다른 정수를 입력받아 가능한 모든 순열 리턴

풀이 1. DFS를 활용한 순열 생성

경우의 수만 구하는건 쉽지만, 문제는 모든 가능한 경우들 자체를 리턴해야하는 것이다.
다음 사진과 같이 DFS를 통해 모든 경우의 수를 탐색하면서 결과를 찾아내는 방법을 구현해 보았다.

def dfs(elements) :
	# 리프 노드일 때 결과 추가
	if len(elements) == 0: 
		results.append(prev_elements[:])
	
	# 순열 생성 재귀 호출
	for e in elements :
		next_elements = elements[:]
		next_elements.remove(e)

		prev_elements.append(e)
		dfs(next_elements)
		prev_elements.pop()

여기서 중요한 부분은 결과를 추가할 때 prev_elements[:] 로 처리해야 한다는 점이다. 파이썬은 모든 객체를 참조하는 형태로 처리되므로 만약 results.append(prev_elements)를 하게 되면 결과 값이 추가되는 게 아니라 prev_elements에 대한 참조가 추가되며, 이 경우 참조된 값이 변경될 경우 같이 바뀌게 된다.
따라서, 값을 복사하는 형태로 참조 관계를 갖지 않도록 처리해야 한다.

풀이 2. itertools 모듈 사용

itertools 모듈은 반복자 생성에 최적화된 효율적인 기능들을 제공하므로, 실무에서는 알고리즘으로 직접 구현하기보다는 이미 잘 구현된 라이브러리를 사용하는 것이 더 효율적이다. 속도도 더 빠른 장점을 지닌다.

def permute(nums) :
	return list(itertools.permutations(nums))

단, 위 코드의 결과는 리스트 내 튜플 형태인 점이 걸린다. 이를 리스트로 변환하려면 다음과 같이 처리해야 한다.

def permute(nums) :
	return list(map(list, itertools.permutations(nums)))

객체 복사 - 중요!

파이썬의 중요한 특징 중 하나는 모든 것이 객체라는 점이다. 숫자, 문자가 리스트, 딕셔너리 같은 객체와의 차이점이라면 불변 객체라는 차이 뿐, 이들마저 모두 객체라고 할 수 있다. 그러니 별도로 값을 복사하지 않는 한, 변수에 값을 할당하는 모든 행위는 값 객체에 대한 참조가 된다.
참조가 되지 않도록 값 자체를 복사하려면 [:] 로 처리하는 방법이다.

>>> a = [1, 2, 3]
>>> b = a
>>> c = a[:]
>>> id(a), id(b), id(c)
(43627, 43627, 43615)

a와 c가 다른 id를 갖는다.

>>> d = a.copy()
>>> id(a), id(b), id(c), id(d)
(43627, 43627, 43615, 43639)

이 경우 변수 d 또한 다른 id를 갖는다. 만약 복잡한 리스트의 경우에는 deepcopy()를 사용해야 한다.

>>> import copy
>>> a = [1, 2, [3, 5], 4]
>>> b = copy.deepcopy(a)
>>> id(a), id(b), b
(43627, 43615, [1, 2, [3, 5], 4])

이처럼 리스트 내에 리스트를 갖는 중첩 리스트도 deepcopy()를 사용하면 문제 없이 값을 복사할 수 있으며, 다른 id를 갖는다.

35. 조합

전체 수 n을 입력받아 k개의 조합을 리턴하라.

풀이 1. DFS로 k개 조합 생성

조합은 순열과는 달리, 자기 자신 뿐만 아니라 앞의 모든 요소를 배제하고 next_elements를 구성한다. 따라서 여기서는 그냥 elements라는 이름으로 다음과 같이 처리한다.

def dfs(elements, start, k) :
	if k == 0:
		results.append(elements[:])
		return
	
	for i in range(start, n + 1) :
		elements.append(i)
		dfs(elements, i + 1, k - 1)
		elements.pop()

풀이 2. itertools 모듈 사용

이 문제도 itertools를 이용해 한 줄 풀이가 가능하다. itertools.permutations()가 있었던 것처럼 itertools.combinations() 도 지원된다.

def combine(n, k) :
	return list(itertools.combinations(range(1, n + 1), k))

풀이 1은 536ms, 풀이 2는 76ms가 걸린다.

36. 조합의 합

숫자 집합 candidates를 조합하여 합이 target이 되는 원소를 나열하라. 각 원소는 중복으로 나열 가능하다.

• 입력

candidates = [2, 3, 6, 7], target = 7

• 출력

[ [7], [2, 2, 3] ]

풀이 1. DFS로 중복 조합 그래프 탐색

조합을 응용한 문제가 이번 문제라 할 수 있다.

def dfs(csum, index, path) :
	...
	for i in range(index, len(candidates)) :
		dfs(csum - candidates[i], i, path + [candidates[i]])
	

dfs() 함수의 첫 번째 파라미터는 합을 갱신해나갈 csum, 두 번째는 순서, 세 번쨰 파라미터는 지금까지의 탐색 경로로 정한다. 종료 조건은 다음 2가지 경우로 정한다.

1. csum < 0 : 목표값을 초과한 경우로 탐색을 종료한다.
2. csum = 0 : csum의 초기값은 target이며, 따라서 csum의 0은 target과 일치하는 정답이므로 결과 리스트에 추가하고 탐색을 종료한다.

나머지 경우는 계속해서 탐색을 시도한다.

def combinationSum(candidates, target) :
	result = []

	def dfs(csum, index, path) :
		# 종료 조건 
		if csum < 0 :
			return
		if csum == 0 :
			result.append(path)
			return

		# 자신부터 하위 원소까지의 나열 재귀 호출
		for i in range(index, len(candidates)) :
			dfs(csum - candidates[i], i, path + [candidates[i]])

37. 부분 집합

풀이 1. 트리의 모든 DFS 결과

경로 path를 만들어 나가면서 인덱스를 1씩 증가하는 형태로 깊이 탐색한다. 부분 집합은 모든 탐색의 경로가 결국 정답이 되므로, 탐색할 때마다 매번 결과를 추가하면 된다.

def subsets(nums) :
	result = []

	def dfs(index, path) :
		# 매번 결과 추가
		result.append(path)

		# 경로를 만들면서 DFS
		for i in range(index, len(nums)) :
			dfs(i + 1, path + [nums[i]])

	dfs(0, [])
	return result

38. 일정 재구성

[from, to]로 구성된 항공권 목록을 이용해 JFK에서 출발하는 여행 일정을 구성하라. 여러 일정이 있는 경우 사전 어휘 순으로 방문한다.

• 입력

[[“JFK”, “SFO”], [“JFK”, “ATL”], [“SFO”, “ATL”], [“ATL”, “JFK”], [“ATL”, “SFO”]]

• 출력

[“JFK”, “ATL”, “JFK”, “SFO”, “ATL”, “SFO”]

풀이 1. DFS로 일정 그래프 구성

중복된 일정일 경우, 어휘 순으로 방문을 해야한다는 점을 주의해야한다.
먼저, 그래프를 구성하는 작업이 필요하다. 다음과 같이 구현 가능하다.

graph = collections.defaultdict(list)
for a, b in tickets :
	graph[a].append(b)
for a in graph :
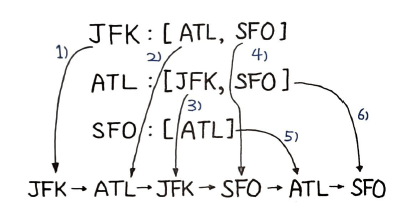
	graph[a].sort()

어휘 순으로 방문해야 하기 때문에 일단 그래프를 구성한 후에 다시 꺼내 정렬하는 방식을 택했다. 위의 입력 예시일 때 그래프 형태는 다음과 같다.

defaultdict(list,
	{'JFK': ['ATL', 'SFO'],
	'SFO': ['ATL'],
	'ATL': ['JFK', 'SFO']})

그런데 이렇게 매번하지 않고 애초에 tickets를 한 번만 정렬해도 결과는 동일하다.
sorted()함수를 이용하면 된다.

graph = collections.defaultdict(list)
for a, b in sorted(tickets) :
	graph[a].append(b)

그 다음엔 pop으로 재귀 호출하면서 모두 꺼내 결과에 추가한다. 결과 리스트에는 역순으로 담기게 될 것 이며, pop()으로 처리했기 때문에 그래프에서는 해다 경로는 사라지게 되어 재방문하게 되지는 않을 것 이다.

def dfs(a) :
	while graph[a] :
		dfs(graph[a].pop(0))
	route.append(a)

어휘순으로 그래프를 생성했기 때문에 pop(0)으로 첫 번째 값을 읽어야 한다. 마지막에는 다시 뒤집어서 어휘 순으로 맨 처음 읽어들였던 값이 처음이 되게 한다. 최종 코드는 다음과 같다.

def findItinerary(tickets) :
	graph = collections.defaultdict(list)
	# 그래프 순서대로 구성
	for a, b in sorted(tickets) :
		graph[a].append(b)

	route = []
	def dfs(a) :
		# 첫 번째 값을 읽어 어휘 순 방문
		while graph[a] :
			dfs(graph[a].pop(0))
		route.append(a)

	dfs('JFK')
	# 다시 뒤집어 어휘 순 결과로
	return route[::-1]

풀이 2. 스택 연산으로 큐 연산 최적화 시도

앞서 풀이에서 큐의 연산을 수행한다고 언급한 바 있다. 파이썬 리스트의 경우 파라미터를 저장하지 않은 값, 즉 마지막 값을 꺼내는 pop()은 O(1)이지만, 첫 번쨰 값을 꺼내는 pop(0)은 O(n)이다. 따라서, 좀 더 효율적인 구현을 위해서 pop(), 즉 스택의 연산으로 처리될 수 있도록 개선하는 게 좋다.

for a, b in sorted(tickets, reverse=True):
	graph[a].append(b)

...
def dfs(a) :
	while graph[a] :
		dfs(graph[a].pop())

이처럼 애당초 그래프를 역순으로 구성하면 추출 시에는 pop()으로 처리가 가능하다.

풀이 3. 일정 그래프 반복

재귀가 아닌 동일한 구조를 반복으로 풀이도 가능하다.

한번 방문했던 곳을 다시 방문하지 않으려면, 별도로 마킹하여 다음번에 방문하지 않거나 아예 스택의 pop()으로 값을 제거하는 방법이 있는데, 여기서는 스택을 이용하므로 다음과 같이 pop()으로 아예 값을 제거한다.

stack = ['JFK']
while stack : 
	while graph[stack[-1]] :
		stack.append(graph[stack[-1]].pop())
	route.append(stack.pop())

그래프에 값이 있다면 pop(0)으로 맨 처음의 값을 추출하여 스택 변수 stack에 넣게 했다. 큐의 연산이다. 이렇게 하면 그래프의 값들은 점점 제거될 것 이며 마지막 방문지가 남지 않을 때까지 while문이 계속 돌면서 위의 그림과 같은 순서대로 처리가 된다.
만약 중간에 끊어지는 입력값들이 주어진다고 해보자.

defaultdict(list, {"JFK": ["KUL", "NRT"], "NRT" : ["JFK"]})

이 경우, JFK -> KUL 에서 더 이상 진행이 불가능하다. 따라서 스택의 값을 다시 pop() 하여 거꾸로 풀어낼 수 있는 또 다른 변수가 필요하다.

route, stack = [], ['JFK']
while stack : 
	while graph[stack[-1]] :
		stack.append(graph[stack[-1]].pop())
	route.append(stack.pop())

이렇게 하면, JKF -> NRT -> JFK -> KUL 순서로 처리가 된다.
전체 코드는 다음과 같다.

def findItinerary(self, tickets) :
	graph = collections.defaultdict(list)
	for a, b in sorted(tickets):
		graph[a].append(b)

	route, stack = [], ['JFK']
	while stack : 
		# 반복으로 스택을 구성하되, 막히는 부분에서 풀어내는 처리
		while graph[stack[-1]] :
			stack.append(graph[stack[-1]].pop())
		route.append(stack.pop())
	return route[::-1]

이 문제의 경우 재귀, 스택 연산, 반복 모두 속도 차이가 거의 없다.
대개는 반복보다는 재귀에 좀 더 높은 점수를 주는 편이며, 재귀로 풀라고 제한하는 경우도 있으므로 재귀 풀이에 좀 더 익숙해지도록 꾸준한 연습이 필요하다.

39. 코스 스케줄

0을 완료하기 위해서는 1을 끝내야 한다는 것을 [0, 1] 쌍으로 표현하는 n개의 코스가 있다. 코스 개수 n과 이 쌍들을 입력으로 받았을 때 모든 코스가 완료 가능한지 판별하라

• 입력

2, [[1, 0]]

• 출력

true

2개의 코스가 있으며 1을 완료하기 위해 0을 끝내면 된다.

풀이 1. DFS로 순환 구조 판별

이 문제는 그래프가 순환 구조인지 판별하는 문제이다.

graph = collections.defaultdict(list)
for x, y in prerequisties : 
	graph[x].append(y)

페어의 첫 번째 값을 x, 두 번째 값을 y로 하되 y는 복수 개로 구성할 수 있게 하다. 이렇게 하면 ‘x’: [‘y1’, ‘y2’] 같은 구조가 된다.

traced = set()
...
for x in graph :
	if not dfs(x) :
		return False

순환 구조를 판별하기 위해 앞서 이미 방문했던 노드를 traced 변수에 저장한다. 이미 방문했던 곳을 중복 방문하게 된다면 순환 구조로 간주할 수 있고 이 경우 False를 리턴하고 종료할 수 있다. 순환구조를 찾기 위한 탐색은 다음과 같이 DFS로 진행한다.

def canFinish(numCourses:  prerequisites) :
	graph = collections.defaultdict(list)

	# 그래프 구성
	for x, y in prerequisites :
		graph[x].append(y)

	traced = set()

	def dfs(i) :
	# 순환 구조이면 False
	if i in traced :
		return False

	traced.add(i)
	for y in graph[i] :
		if not dfs(y) :
			return False

	# 탐색 종료 후 순환 노드 삭제
	traced.remove(i)

	return True

	for x in list(graph) :
		if not dfs(x) :
			return False

	return True

풀이 2. 가지치기를 이용한 최적화

위의 풀이를 좀 더 효율적으로 만들 수 있다. 한 번 방문했던 그래프는 두 번 이상 방문하지 않도록 무조건 True로 리턴하는 구조로 개선하면 시간을 획기적으로 줄일 수 있다.

def canFinish(numCourses, prerequisites) :
	graph = collections.defaultdict(list)

	# 그래프 구성
	for x, y in prerequisites :
		graph[x].append(y)

	traced = set()
	visited = set()

	def dfs(i) :
		# 순환 구조이면 False
		if i in traced :
			return False
		# 이미 방문했던 노드이면 True
		if i in visited :
			return True

		traced.add(i)
		for y in graph[i] :
			if not dfs(y) :
				return False

		# 탐색 종료 후 순환 노드 삭제
		traced.remove(i)
		# 탐색 종료 후 방문 노드 추가
		visited.add(i)
	
		return True

	# 순환 구조 판별
	for x in list(graph) :
		if not dfs(x) :
			return False

	return True

이런식으로 가지치기를 이용하면 920ms 에서 96ms로 시간을 줄일 수 있다.

defaultdict 순회 문제

for x in list(graph) :

graph를 순회할 때 list 로 감싸지 않으면 Runtime Error: dictionary changed size during iteration 이 뜨게 된다. graph 딕셔너리를 최소 생성 후 변경한 적이 없는데 이런 에러가 뜬다.

graph = collections.defaultdict(list)

위의 코드가 문제이다. 존재하지 않는 키를 조회할 때 오류를 내지 않기 위해 항상 디폴트를 생성하는 구조로 되어 있다는 점이다. 따라서 다음과 같은 반복문에서 graph 값이 변경된다는 오류가 발생한다.

for x in graph : 
	...

해당 반복문이 제대로 실행되려면 graph 변수를 defaultdict() 에서 분리해서 고정시킬 필요가 있다. 3.7+의 해결 방식을 보면 list() 로 묶어서 해결하라는 답변을 볼 수 있다.
즉, 새로운 복사본을 만들어야 한다는 뜻이다.