파이썬 알고리즘 인터뷰 책의 3부 7장을 읽고 나서 그 내용을 정리해보았다.
07. 두 수의 합
매우 쉬운 난이도의 문제에 속하지만, 최적화할 수 있는 여러 가지 방법이 숨어 있어서 코딩 인터뷰 시 높은 빈도로 출제가 된다고 한다.
풀이 1. 브루트 포스로 계산
배열을 2번 반복하면서 모든 조합을 더해서 일일이 확인해보는 무차별 대입 방식인 브루트 포스(Brute-Force) 로 문제를 해결하였다.
시간복잡도가 O(n^2) 이고 5,284ms나 소요된다. 굉장히 비효율적인 방법이여서 좀 더 최적화할 수 있는 방법들을 살펴보았다.
풀이2. in 을 이용한 탐색
def twoSum(self, nums: List[int], target: int) -> List[int]:
for i, n in enumerate(nums) :
complement = target - n
if complement in nums[i + 1:] :
return [nums.index(n), nums[i + 1:].index(complement) + (i + 1)]in 의 시간복잡도는 O(n) 이여서 이전과 동일한 O(n^2)이지만 같은 시간복잡도라도 in 연산쪽이 훨씬 더 가볍고 빠르다.
이 풀이의 경우 파이썬의 내부 함수로 구현된 in 은 파이썬 레벨에서 매번 값을 비교하는 것에 비해 훨씬 더 빨리 실행된다.
실제로 864ms 만에 실행이 가능하다.
풀이3. 첫 번째 수를 뺸 결과 키 조회
def twoSum(self, nums: List[int], target: int) -> List[int]:
nums_map = {};
# 키와 값을 바꿔서 딕셔너리로 저장
for i, num in enumerate(nums) :
nums_map[num] = i
# 타켓에서 첫 번째 수를 뺀 결과를 키로 조회
for i, num in enumerate(nums):
if target - num in nums_map and i != nums_map[target_num] :
return [i, nums_map[target - num]] 타켓에서 첫 번쨰 수를 빼면 두 번쨰 수를 바로 알아낼 수 있다.
딕셔너리는 해시 테이블로 구현되어 있고, 이 경우 조회느 평균적으로 O(1)에 가능하다. 불과 48ms 만에 실행된다.
풀이4. 조회 구조 개선
딕셔너리 저장 과 조회를 2개의 for문으로 각각 처리했던 방식을 좀 더 개선해서 하나의 for문으로 합친 풀이이다.
굳이 전체를 모두 저장하지 않고도 정답을 찾게 되면 함수를 바로 빠져나올 수 있는 장점이 있다. 그러나, 두 번째 값을 찾기 위해 어차피 매번 비교해야 하기 때문에
앞의 풀이와 성능은 비슷하다.
def twoSum(self, nums: List[int], target: int) -> List[int]:
nums_map = {}
# 하나의 for문으로 통합
for i, num in enumerate(nums) :
if target - num in nums_map :
return [nums_map[target - num], i]
nums_map[num] = i실행속도가 44ms 이므로, 앞의 풀이와 큰 차이가 없다. 그러나 한결 코드가 간결해졌다.
풀이5. 투 포인터 이용
양쪽 끝에서 2개의 포인터를 이용하여 두 수의 합을 타켓과 비교하면서 포인터를 이동시키는 방식이다.
def twoSum(self, nums: List[int], target: int) -> List[int]:
left, right = 0, len(nums) - 1
while not left == right:
# 합이 타켓보다 작으면 왼쪽 포인터를 오른쪽으로
if nums[left] + nums[right] < target:
left += 1
# 합이 타켓보다 크면 오른쪽 포인터를 왼쪽으로
elif nums[left] + nums[right] > target :
right -= 1
else :
return [left, right]
투 포인터의 시간 복잡도도 O(n) 이다. 하지만 이 풀이가 제대로 작동하려면 배열이 정렬된 상태여야 한다.
하지만 우리는 인덱스를 찾아야하는데, 정렬을 해버리면 인덱스가 섞여버리기 때문에 곤란해진다.
08. 빗물 트래핑
풀이 1. 투 포인터를 최대로 이동
이 문제는 높이와 너비 모든 공간을 차례대로 모두 살펴보면 O(n^2)에 풀이가 가능하다.
그러나, 너무 비효율적이기 때문에 효율적인 방법을 활용해야한다. 투 포인터나 스택으로 O(n) 풀이가 가능하다.
def trap(self, height: List[int]) -> int :
if not height:
return 0
volume = 0
left, right = 0, len(height) - 1
left_max, right_max = height[left], height[right]
while left < right :
left_max, right_max = max(height[left], left_max),
max(height[right], right_max)
# 더 높은 쪽을 향해 투 포인터 이동
if left_max <= right_max :
volume += left_max - height[left]
left += 1
else :
volume += right_max - height[right]
right -= 1
return volume아직 완벽히 이해가 되지 않아서 다시 한번 봐야 할 것 같다.
풀이 2. 스택 쌓기
스택을 쌓아 나가면서 현재 높이가 이전 높이보다 높을 때, 즉 꺾이는 부분 변곡점을 기준으로 격차만큼 물 높이를 채운다.
한 번씩만 조회하기 때문에 마찬가지로 O(n)에 풀이가 가능하다.
def trap(self, height: List[int]) -> int :
stack = []
volume = 0
for i in range(len(height)) :
# 변곡점을 만나는 경우
while stack and height[i] > height[stack[-1]] :
# 스택에서 꺼낸다.
top = stack.pop()
if not len(stack) :
break
# 이전과의 차이만큼 물 높이 처리
distance = i - stack[-1] - 1
waters = min(height[i], height[stack[-1]]) - height[top]
volume += distance * waters
stack.append(i)
return volume이 문제는 상당히 어려운 문제이다. 특히 스택 쌓기 풀이는 직관적으로 떠올리기가 쉽지 않을 뿐더러 풀이 방법 또한 많이 고민해봐야겠다.
09. 세 수의 합
풀이 1. 브루트 포스로 계산
O(n^3) 이 걸리겠지만, 타임아웃이 발생할 것 이다. 이 문제는 시간복잡도를 O(n^2) 으로 줄이기를 요구할 것 이다.
우선 배열을 정렬해준다. 팀소트의 .sort() 를 이용하면 되고, O(nlogn) 이 걸린다.
삼중 for문을 순회하면서, 중복된 값이 있을 수 있으므로 이 경우 다음과 같이 continue 로 건너뛰도록 처리해준다.
if i > 0 and nums[i] == nums[i - 1] :
continue결국 타임아웃이 발생한다. O(n^2) 이내로 최적화 할 수 있는 방법을 찾아야 한다.
풀이 2. 투 포인터로 합 계산
i를 축으로 하고, 중복된 값을 건너뛰게 한 부분은 앞의 풀이와 동일하다.
for i in range(len(nums - 2)) :
if i > 0 and nums[i] == nums[i - 1] :
continuei의 다음 지점과 마지막 지점을 그림과 같이 left, right 로 설정하고 간격을 좁혀가면서 sum 을 계산하는 방식이다.
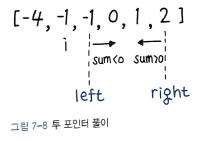
앞의 풀이가 타임아웃이 발생한다면, 이 풀이는 884ms가 걸린다.
투 포인터
시작점과 끝점 또는 왼쪽 포인터와 오른쪽 포인터 두 지점을 기준으로 하는 문제 풀이 전략을 뜻한다.
범위를 좁혀나가기 위해서는, 일반적으로 배열이 정렬되어 있을 때 좀 더 유용하다.
10. 배열 파티션 I
n개의 페어를 이용한 min(a, b)의 합으로 만들 수 있는 가장 큰 수를 출력하라.
풀이 1. 오름차순 풀이
처음에는 이해가 잘 안되었는데, 찬찬히 이해해보니 결국 min()이 되도록 커야한다는 뜻이고 뒤에서부터 내림차순으로 집어넣으면 항상 최대 min() 페어를 유지할 수 있다.
정렬된 상태 에서 앞에서부터 오름차순으로 인접 요소 페어 를 만들면 가장 큰 a1 과 a2 페어들을 만들 수 있고 이 페어들의 합이 곧 만들 수 있는 최대합이 된다. 332ms 가 걸린다.
풀이 2. 짝수 번째 값 계산
사실 페어에 대해 일일이 min 값을 구하지 않아도 짝수 번째 값(0부터 시작하므로)을 더하면 더 빠르게 해결가능하다.
def arrayPairSum(list) :
sum = 0
nums.sort()
for i, n in enumerate(nums) :
# 짝수 번째 값 계산
if i % 2 == 0:
sum += n
return sum
실행시간은 308ms 이다.
풀이 3. 파이썬다운 방식
풀이 2의 코드를 슬라이싱 을 활용하면 한 줄로 풀이가 가능하다.
def arrayPairSum(list) :
return sum(sorted(nums)[::2])슬라이싱 구문 [::2] 는 2칸씩 건너뛰므로 짝수 번째 값을 계산하는 것과 동일하다. 284ms가 걸린다.
11. 자신을 제외한 배열의 곱
배열을 입력받아 output[i] 가 자신을 제외한 나머지 모든 요소의 곱셈 결과가 되도록 출력하라.
단, 나눗셈을 하지 않고 O(n)에 풀이하라.
풀이 1. 왼쪽 곱셈 결과에 오른쪽 값을 차례대로 곱셈
여기서 이 제약사항 때문에, 미리 전체 곱셈 값을 구해놓고 각 항목별로 자기 자신을 나눠서 풀이하는 방법은 안된다는 뜻이다. 그렇다면, 자기 자신을 제외하고 왼쪽의 곱셈결과와 오른쪽의 곱셈 결과를 곱하는 수밖에 없다.
def productExceptSlef(nums) :
out = []
p = 1
# 왼쪽 곱셈
for i in range(0, len(nums)) :
out.append(p)
p = p * nums[i]
p = 1
# 왼쪽 곱셈 결과에 오른쪽 값을 차례대로 곱셈
for i in range(len(nums) - 1, 0 - 1, -1) :
out[i] = out[i] * p
p = p * nums[i]
return out12. 주식을 사고팔기 가장 좋은 시점
한 번의 거래로 낼 수 있는 최대 이익을 산출하라.
풀이 1.브루트 포스로 계산
가장 저점에 사서 고점에 팔면 최대 이익을 낼 수 있다.
처음부터 O(n^2), 즉 브루트 포스 기반으로 사고팔고를 반복하면 마지막에 최대 이익을 산출 가능하다.
def maxProfit(prices) :
max_price = 0
for i, price in enumerate(prices) :
for j in range(i, len(prices)) :
max_price = max(prices[j] - price, max_price)
return max_price하지만, 안타깝게도 타임아웃이 발생한다.
풀이 2. 저점과 현재 값과의 차이 계산
현재값을 가리키는 포인터가 우측으로 이동하면서 이전 상태의 저점을 기준으로 가격 차이를 계산하고, 만약 클 경우 최댓값을 계속 교체해나가는 형태로 O(n) 풀이가 가능해진다.
profit = -sys.maxsize
min_price = sys.maxsize최댓값이 되어야 할 profit 변수와 최솟값이 되어야 할 min_price 변수의 초깃값은 이처럼 각각 시스템의 가장 작은 값, 가장 큰 값으로 정한다.
이렇게 하면 어떤 값이 들어오든 바로 교체될 수 있기 때문이다. 만약 None 으로 잡아두게 되면 비교 시 타입 에러가 발생할 수 있으므로 최솟값, 최댓값은 시스템의 최댓값, 최솟값으로 설정하는게 편하다.
단, 이 문제에서는 최대 이익 profit이 나중에 최종 결과로 리턴되는데, 입력값이 [], 즉 빈 배열인 경우에는 -sys.maxsize가 그대로 리턴될 수 있기 떄문에, profit 을 0으로 설정해준다.
def maxProfit(prices) :
profit = 0
min_price = sys.maxsize
# 최솟값 & 최댓값을 계속 갱신
for price in prices :
min_price = min(min_price, price)
profit = max(profit, price - min_price)
최댓값과 최솟값
이 둘의 값을 지정하는 방법에는 여러 가지가 있다. 앞서 문제 풀이에서 sys 모듈을 사용하면 시스템이 지정할 수 있는 가장 높은 값, 낮은 값을 사용가능하다.
mx = -sys.maxsize
mn = sys.maxsizefloat() 을 이용해 다음과 같이 무한대 값을 지정하는 방법도 있다.
mx = float('-inf')
mn = float('inf')가장 좋지 않은 방법은 99999999와 같은 임의의 값을 지정하는 것이다.
mn = 9999999파이썬의 숫자형은 임의 정밀도를 지원하며 사실상 무한대의 값을 지정할 수 있다.
보통 코딩 테스트 플랫폼에서는 문제에 n은 0 < n < 5000 사이의 값이다 와 같은 입력값의 제약 조건이 기술되어 있다.
이 기준에 맞춰 최댓값과 최솟값을 처리하면 된다.
